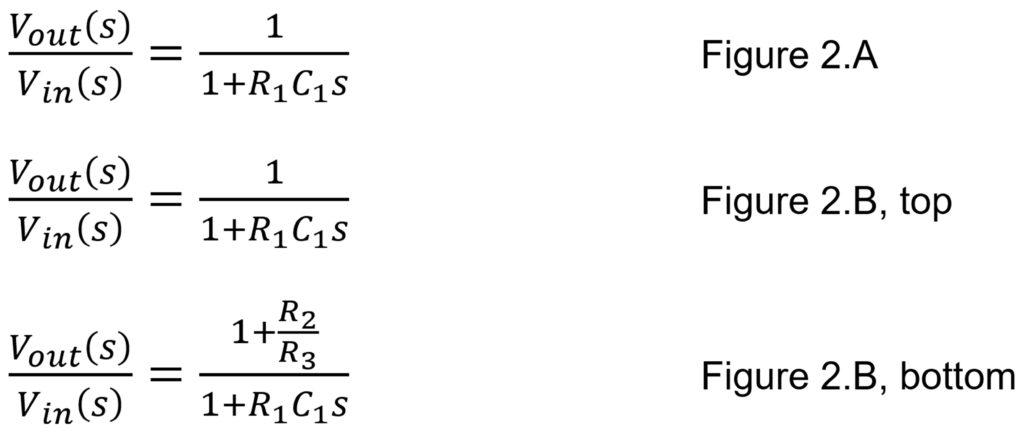The practical magical first-order analog filter

Finding the right analog filter to build a sensor circuit doesn’t have to be complicated. Understandably, the plethora of filter options can be overwhelming. Also, selecting a less-than-ideal filter may result in compromises, potentially increasing system cost, or affecting performance. To help simplify filter selection, this series of blogs explore key considerations when assessing your system’s analog filter needs and available devices. For this, we will start with the 1st order low-pass analog filter discussion.

1^storder low-pass filter applications

A low-pass filter attenuates higher frequency signals above the three-decibel (3dB) corner frequency. In the frequency domain, the 1^st order low-pass filter response at its output allows DC to low-frequency signals to transmit in the passband (Figure 1).

Figure 1. A 1st order, low-pass filter frequency response with an initial magnitude of 0 dB and a 3dB corner frequency at 1 kHz. (Image: Analog Devices)

Figure 1, from Analog Devices Analog Filter Wizard, represents the frequency response of a 1^st order 1 kHz low-pass filter. With the diagram, the magnitude (y-axis) starts at 0 dB through the passband, and with increased frequency, starts to attenuate at 1 kHz (x-axis). At 1 kHz, the low-pass filter Magnitude is -3 dB. Beyond 1 kHz, the filter attenuation characteristic is -20 dB per frequency decade or -20 dB/decade. Note that at 10 kHz, the filter magnitude is -20 dB, and at 100 kHz, the filter magnitude is -40 dB.

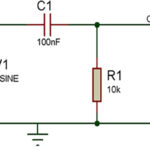
The circuit diagram for a 1^st order filter can be passive with a resistor and capacitor or active with a resistor, capacitor, and operational amplifier (Figure 2).

Figure 2. The input of the passive low-pass filter (A) has R1 and C1 filter elements. Two active non-inverting low-pass filters (B) uses the same input structure with the following amplifier in a gain configuration. The active inverting low-pass filter (C) uses R2 and C1 in the feedback loop to implement the filter corner frequency. (Image: Bonnie Baker)

The transfer function Figure 2’s circuits are below.

In all 1^st order low-pass filters, the pole frequency equals:

In Figure 2, R1 and C1 equaling 159.15 kW and 1 mF, create a 1 kHz pole.

1^st order low-pass filter applications

The 1^st order low-pass filter can come in handy in numerous applications. The idea is to make sure that you are attenuating enough of the higher frequency noise in your application and to use the resistive and capacitive devices to your advantage.

The amplifier interface to a standard SAR analog-to-digital converters (ADC) utilizes a 1^st order low-pass filter (Figure 3).

Figure 3. The placement of 1st order low-pass filter is very effective with a SAR-ADC converter. (Image: Bonnie Baker)

In Figure 3, the 1^st order filter’s capacitor absorbs current spices from the SAR’s internal switch, S₁. Proper selection of the R_IN resistor brings stability to the driver amplifier’s response.

High-precision SAR-ADCs require a high-precision, buffered voltage reference. The 1^st order filter’s design for a SAR-ADC voltage reference interface ensures the stability of the reference’s driver amplifier (Figure 4).

Figure 4. For High precision SAR-ADCs there is a buffered voltage reference with amplifier stability passive capacitive devices. (Image: Bonnie Baker)

The resistive element of this 1^st order filter is C_L1‘s parasitic resistance (effective-series-resistance, ESR) stabilizes the voltage reference driver amplifier. The second capacitor, C_L2, absorbs the ADC’s switching noise.

A delta-sigma ADC also requires a 1^st order low-pass filter at its input. (Figure 5).

Figure 5. To obtain a high 24-bit resolution, a low-pass input filter to the ADC reduces high-frequency digital filter images. (Image: Bonnie Baker)

This passive filter removes high-frequency digital filter signal reflections.

Since a delta-sigma converter is a sampling system, all noise and signals above ½ of the modulator’s sampling frequency aliases back (Figure 6). The digital filter attenuates the higher frequency noise except around the sampling frequency.

Usually, the amplitude of the noise and signal hovering around the sample rate is small, but noise is a reality, and it will be present in your circuit. To make this interesting, you have a high-resolution converter that shows the noise in its lower bits. This is why you’ll need a continuous-time filter in front of the delta-sigma converter.

In Figure 6, the lowest value for your analog filter, corner frequency, should be Fd. Fortunately, the required strength of this filter is low, and a simple 1^st order low-pass filter is usually good enough.

Do I need a high-pass filter in my circuit instead?

The 1^st order low-pass filter is helpful for a multitude of applications. However, there are instances where your system may require a high-pass filter. Read on to Part 2 of this blog filter series.

Filter Design Tools
“Analog Filter Wizard”, Analog Devices
“Filter Design Tool”, Texas Instruments