In the previous tutorial, sound waves and their properties were discussed. Now, let’s learn about acoustic waves.
Sound waves typically refer to frequencies that are audible to humans, which are in the 20 Hz to 20 kHz range. However, waves with frequencies that are greater than 20 kHz are ultrasonic waves. And, those in the gigahertz (or higher) range are called hypersonic waves.
Generally, the term “acoustic wave” is used in reference to a sound or vibration of any frequency. This makes sense because in physics, acoustics is the study of any mechanical wave in the solid, liquid, or gaseous medium. These are longitudinal waves, which move in the same direction of vibration as their direction of travel. The source of these waves is the vibration produced in any medium or sound source.
Since sound waves are also generated by the vibration from a medium, it follows that acoustic waves are a type of sound waves that travel on a surface, liquid, or in a gaseous medium.
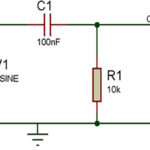
Here are a few depictions…



By studying sound as an acoustic wave, we can better understand its mechanical properties.
Acoustic waves are characterized by the following physical properties…
- Acoustic or sound pressure
- Particle velocity
- Acoustic or sound intensity
- Particle displacement
Let’s review each one…
Acoustic or sound pressure
The pressure that’s generated by any surrounding sound waves. Sound pressure is the deviation in the equilibrium atmospheric pressure due to a sound wave and it’s measured in pascal (Pa) or N/m2.
When a sound wave travels through a medium, it creates a disturbance in that medium’s pressure — increasing its total pressure.
This is expressed by an equation:
Ptotal = P1 +Ps
Where…
Ptotal = Total pressure in the medium
P1 = Pressure generated by the sound wave
Ps = Static or equilibrium pressure
The increase of pressure can be measured by using a microphone in an air medium or a hydrophone in the water.
Particle velocity
The velocity of a wave particle in a particular medium, which is measured in m/s. Imagine that a sound wave is traveling through a liquid medium. In this case, the particle velocity is the velocity of the liquid as the sound wave causes the particles to move back and forth per the vibration in the wave.
However, the particle velocity is not the same for the liquid and the sound wave. A sound wave travels much faster than a particle in this medium.
The particle velocity can be calculated using this equation:
v = dδ/dt
Where…
v = Particle velocity
δ = Particle displacement
Acoustic or sound intensity
Together, the sound pressure and the particle velocity make up the sound intensity. It’s defined as the power transfer per unit area. This area is always perpendicular to the energy that’s transferred.
Therefore, the sound intensity is the power that’s transferred by a sound wave per unit area, and it’s measured in watt per square meter or W/m2.
The sound intensity can be calculated as follows:
Sound intensity, I = p*v
Where…
p = Sound pressure
v = Particle velocity
Particle displacement
The displacement of a particle from its original position is called when sound travels through a medium. Particle displacement is measured in meters.
When a sound wave travels through the air, the particles in the air experience displacement, depending on the particle velocity. Displacement can either occur in the direction of the sound wave or opposite to it.
Particle displacement is calculated by this equation:
V = dδ/dtδ
Where…
v = Particle velocity
dt = Time period
A basic understanding of these mechanical properties of sound is useful when working with audio transducers. The most common audio input transducer is a microphone and the most common audio output transducer is a speaker.
In the next tutorial, we’ll take a look at microphones, including how they work and how they’re classified.