Antennas based on fractal mathematics offer some significant advantages but also some controversy.
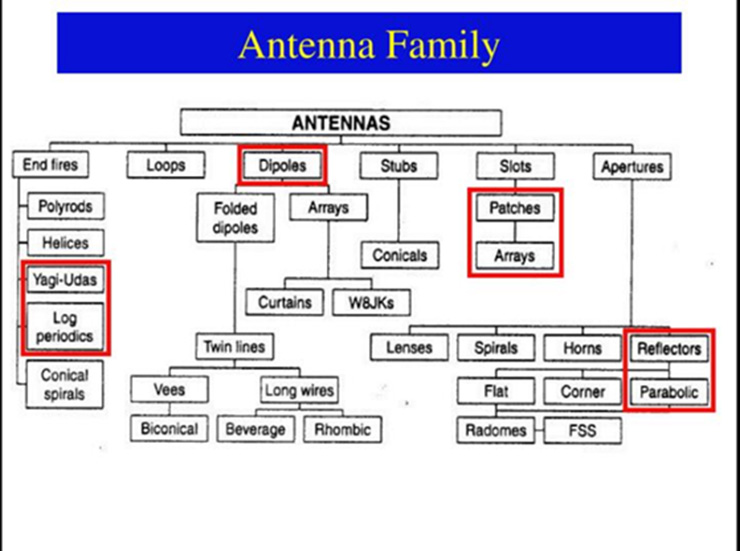
Although all antenna designs are derived from either the basic dipole or monopole/ground-plane configurations, there are almost countless antenna variations in use (Figure 1). Each one offers a different combination of key attributes such as center frequency, bandwidth, bandwidth, side lobes, front-to-back ratio, efficiency, size, cost, ruggedness, and more.
But there’s one antenna implementation that is less well known and often overlooked yet has been designed for applications such as space-constrained smartphones: the fractal antenna. This FAQ will explore the principles behind this antenna and some of the issues associated with it.
Q: What are “fractals,” anyway?
A: Fractals are a class of geometric forms that evolve and replicate internally over multiple iterations. One semi-formal definition is that they are various extremely irregular curves or shapes for which any suitably chosen part is similar in shape to a given larger or smaller part when magnified or reduced to the same size. In colloquial terms, fractals are self-similar whether you view them from close up or very far away; for example, just as a stone at the base of a foothill resembles in miniature the mountain from which it originally tumbled down. They can be based on basic geometrical forms or more complex shapes (Figure 2).
Q: How are fractals generated?
A: They can be generated “by hand,” and there are many examples of fractal images in Hindu temples and Islamic mosques. Now they are often created by applying iterative methods to solving non-linear or polynomial equations.
Q: When were fractals “discovered?”
A: It depends on what you mean by “discovered.” Fractals have been studied by mathematicians informally since the late 1800s, but they did not have a widely presented formal analysis until 1982 when French American mathematician Benoit Mandelbrot published a breakthrough book “The Fractal Geometry of Nature,” (Figure 3) based on his shorter earlier work in French “Les Objets Fractals: Forme, Hasard et Dimension,” as part of his investigation into what he termed the “roughness and self-similarity” in nature.
Q: What did he investigate?
A: He identified that there are some geometric shapes which he called “fractals,” that are equally “rough” at all scales. No matter how close you look, they never get simpler, much as the section of a rocky coastline you can see at your feet looks just as jagged as the stretch you can see from space. In effect, there are smaller and smaller copies of a pattern successively nested inside each other, so that the same intricate shapes appear no matter how much you zoom in to the whole.
Q: Are fractals only conceptual, mathematical constructs?
A: No, they also appear in nature with fern leaves and Romanesque broccoli as just two examples. Of course, many are now generated using computer algorithms and as computers have become more powerful, the intricacy and complexity of the fractals they can generate has increased significantly.

Q: Why call them fractals?
A: The term “fractal” was coined by Mandelbrot in 1975. It comes from the Latin fractus, meaning an irregular surface like that of a broken stone or broken glass.
Q: Are fractals discussed extensively in the literature?
A: Since the publication of Mandelbrot’s book, there have been thousands of articles and videos on fractals ranging from artistic to tutorial to mathematically intense works
Q: Is there just one type of fractal?
A: No, they can be divided into various subgroups depending on how they are generated and their “seed” image. One group is named the Mandelbrot Set, but there are many others.
Q: What are the main classes of fractals?
A: Fractals can be classified into two categories: deterministic and random.
Deterministic fractals are generated by iterations using increasingly scaled-down rotated copies of themselves. Such fractals can be generated using computer graphics that are repeatedly mapped out by a recursive algorithm. Random fractals also contain elements of randomness that allow the simulation of natural phenomena. While they relate to nature and are visually fascinating, they are not used for antennas.
Q: What are some examples of deterministic fractals?
A: Two basic examples are the Koch snowflake (or Koch fractal loop), Figure 4, and the Minkowski Island fractal, Figure 5. The geometry-generating process begins with a basic geometry known as the initiator (the triangle and the square, respectively). For the Koch snowflake, the middle third of each triangle is replaced by a generator, and for the Minkowski Island, each of the four sides of the square is replaced by a generator.
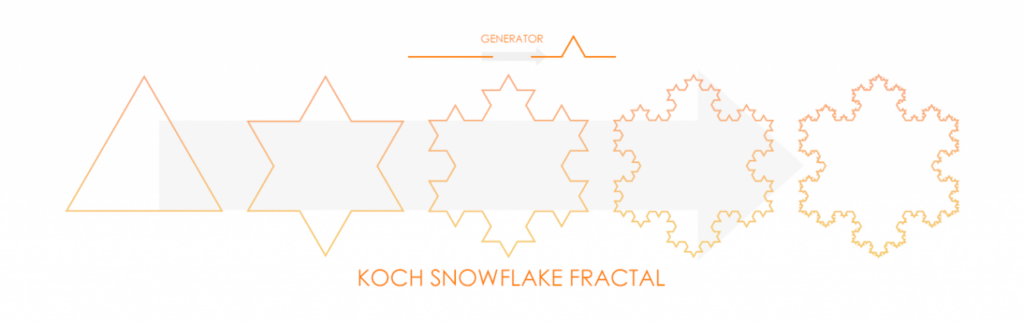

They can even be combined as a Koch/Minkowski fractal, Figure 6.

The next section will look at fractals in the context of antenna design.
Related WTWH content (These are only tutorials; there are also many product-related announcements)
Demonstrating antenna diversity, Part 1: The challenges
Demonstrating antenna diversity, Part 2: The PIFA
Demonstrating antenna diversity, Part 3: The Yagi antenna
What materials can be used to make miniature antennas?
The basics of dielectric resonator antennas
How distributed antenna systems bring cellular indoors
Getting one wire to do more, Part 4 – headphone wire as antenna
Getting one wire to do more, Part 3 – Powering the antenna LNA
Software tool helps designers place antennas in design
5 tips for designing with embedded antennas
Metamaterials, mmWave antennas, 3D radar and holographic beamforming
mmWave antennas and antenna management for 5G
The microstrip antenna, Part 1: Basics
The microstrip antenna, Part 2: Implementation
External references
Jem Engineering, “Fractal Antennas, Explained”
IEEE Insight, “Why Mobile Phones Can Do So Many Things: The Invention of The Fractal Antenna”
Antenna-Theory, “Fractal Antenna”
U.S. Patent 6,452,553, “Fractal Antennas and Fractal Resonators”
The Oracles Library, “Sacred Geometry: How Cell Phones Work Using Fractals”
Yale University, “Fractal Geometry”
Peter Joseph Bevelacqua Ph.D. thesis, “Antenna Arrays: Performance Limits and Geometry Optimization”
Wikipedia, “Fractal Antenna”
Wikipedia, “Benoit Mandelbrot”
Hackaday, “Fractals Among Us”
Wikipedia, “Sierpiński carpet”