Part 1 of this FAQ looked at the basic principles of the GPS system. Part 2 looks at some hardware circuitry used to implement a GPS receiver as well as the unappreciated role that Einstein’s Theory of Special Relativity plays in providing an accurate GPS.
Q What are the key elements of a GPS receiver?
A: As with any receiver, the signal path begins with a mostly analog RF front end, consisting of an antenna, low-noise amplifier (LNA), and filters. In the case of the GPS receiver, there is also a specialized, high-performance data-processing engine or core which performs the extensive calculations needed to transform the demodulated and time-aligned PRSQ into actual position information.
Q: What is in the analog signal-chain front end?
A: The front end is an application-specific receiver which may use the well-known superheterodyne architecture or other down-conversion approach. Unlike general-purpose receivers, it does not have to tune across multiple carrier channels or deal with various bandwidths and modulation types. Instead, it is tightly focused on the two GPS carrier frequencies and the modulation format for the encoded signals.
Q: How important is the front-end preamplifier (if any) and LNA?
A: As expected, very important. The GPS received-signal level is very low, on the order of -160 dBm. Therefore, most designs use an antenna-mounted preamp if the antenna is mounted any distance from the rest of the receiver, to maintain SNR and minimize the effect of noise pickup between antenna and LNA.
Q: How is a typical GPS receiver front end implemented?
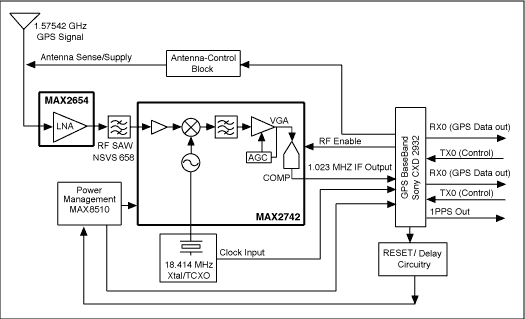
A: The first GPS receivers used small-scale ICs and discrete transistors to capture the received signal. As the demand for GPS increased and as the IC process technology advanced, IC vendors were able to put nearly all the analog signal-chain circuitry into a single IC such as the Maxim MAX2742 Single-Chip Global Positioning System Receiver Front-End, Figure 1, which includes a LNA and mixer, IF section, digital sampler, and local oscillator synthesizer. This IC has a front-end noise figure of 4.5 dB, does not need any external IF SAW or discrete filters, and requires just 32 mW of power from a +2.4 V to +3.6 V supply.
Q: What about the numeric-processing functions?
A: The MAX2742 does not do that function; instead, it passes the decoded GPS to a processor of the user’s choice. Some designers prefer to use a processor that is already in the product, if it has the available processing power, or have algorithms already coded and tested on a specific processor or FPGA.
Q: Are there single-chip solutions?
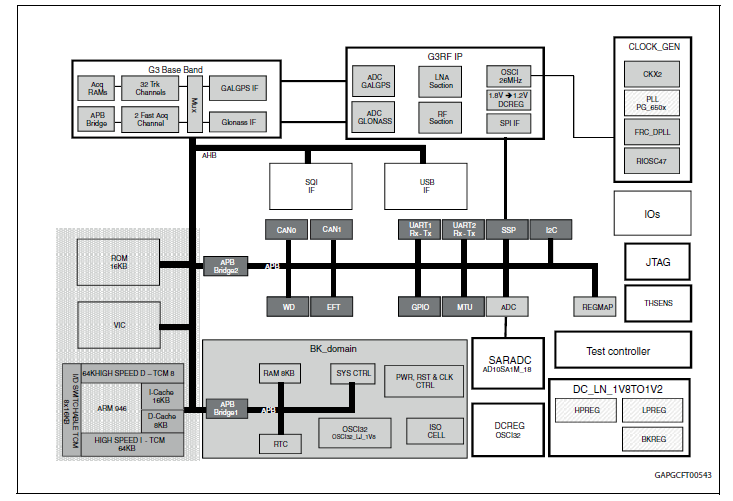
A: Yes, there are many, such as the STA8088CWG from STMicroelectronics. This IC contains not only the analog front end, but the entire computational engine, Figure 2. It is more than a GPS-only IC; it is a multi-GNSS IC as well, handling GPS/Galileo/Glonass/QZSS constellations and formats which is attractive in many cases. The embedded ARM946 MCU operates at up to 208 MHz and handles the calculations. The IC also includes all needed peripheral functions such as timers, I/O, and interfacing with a system controller.
Q: What supports this type of IC?
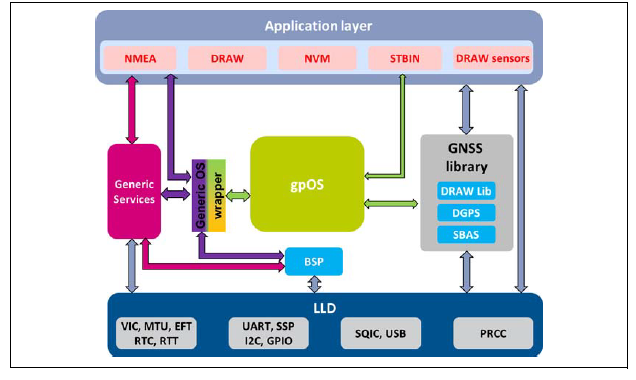
A: ICs such as the STA8088CWG are complicated “systems on a chip.” To this end, the vendor also offers a package of code libraries and development tools, Figure 3, so designers can pick what they need, customize the code if needed, and tailor the final version to the application requirements.
Q: What is TTFF – it is often cited on GPS data sheets?
A: In addition to accuracy, GPS users are often, but not always, concerned with a specification called Time To First Fix. This defines how long it takes for the GPS receiver to establish a first valid position result after it has acquired signals from at least four satellites. Depending on the end-application, product developers may put extra effort into fine-tuning the algorithms which determine position in order to reduce TTFF. Typical TTFF time is between 30 and 120 seconds.
Q: What sort of algorithms are employed to determine position from the decoded, time-aligned signals?
A: They are intensive, extensive, and too complicated to review here, as they involved many subtleties and advanced calculations. These must be implemented carefully and are usually done using 64-bit floating-point arithmetic. The reason is that what may seem like trivial rounding errors and truncation effects can introduce significant errors in the final answer, since there are so many calculations cycles resulting in error buildup over the cycles. Calculations are done in polar coordinates, referenced to an Earth-centered frame, as this is compatible with the circular nature of the orbits and earth’s surface.
Q: Can you give an example of some of the subtleties involved in GPS calculations?
A: That’s easy: corrections and adjustments must be made because of effects identified by Einstein’s Theory of Special Relatively (if you are not familiar with the concepts and conclusions of special (not general) relativity — you should be!). Although the average non-technical person might say that Einstein’s relativity principles have no impact on their daily life, the reality is that without the insight it provides, GPS results would be in error by anywhere from a few miles to tens of miles. That would leave GPS still somewhat useful for navigation at sea or on long flights, but useless for street-by-street navigation.
Q: How does relativity affect GPS data and subsequent results?
A: In many ways, including these:
- Due to the height of the orbit (about 20,000 km), the GPS satellites are at a lower gravitational potential than clocks are at the Earth’s surface; the result is that their atomic clocks run slower and are shifted in frequency.
• Due to their continuous acceleration, as they orbit, the satellites’ clocks experience time dilation and, again, run slower than on Earth.
• The Earth’s rotation relative to a GPS satellite’s orbit affects their relative paths and timing relationships.
• The satellites’ orbits are not perfect circles; they are elliptical, so the variations are also cyclical. This means that a mere 1% eccentricity in orbit results in a 28-nanosecond timing variation.
• Everything is moving with respect to everything else: Earth-based receivers move with respect to a single satellite and the satellites move with respect to each other. This makes it difficult to establish a frame of reference and remain consistent within it.
Q: Are there issues that haven’t been raised in this FAQ?
A: Absolutely! There are many more issues that could have been explored or discussed. One thing to think about is this: how do you test your GPS receiver’s performance, including factors such as RF sensitivity, immunity to noise and fading, and the accuracy of its algorithms? After all, you don’t have a test-bench equivalent to a constellation of satellites you can access and control!
Q: Can GPS be used for anything else besides navigation and position determination?
A: Yes, it has been used as the basis for a world-wide time base; that is one of the fortuitous and unforeseen applications. Because the satellite clocks are so precise and are synchronized to each other, and they are accessible from anywhere, special receivers have been devised and are widely available which capture and extract the clock timing. The result is the ability to synchronize widely dispersed Earth-based clocks worldwide to within a few nanoseconds, an achievement which was previously impossible or very difficult.
This FAQ has explored the basics of GPS and GNSS functions. The references below provide more details, and there are hundreds of other references available online, in technical journals, and in books. These span basic, less-technical explanations to highly detailed, analytical works. Reference 1 is the official U.S. Government GPS site and has both explanatory sections as well as formal technical documents.
References:
- GPS: The Global Positioning System (Official US Government Site)
- “Relativistic Effects in the Global Positioning System,” July 18, 2006.
- “Relativity in the Global Positioning System,” Living Reviews in Relativity, January 2003.
- “Relativity and the Global Positioning System,” Physics Today, May 2002.
- Richard H. Battin, “An Introduction to the Mathematics and Methods of Astrodynamics,” ISBN: 978-1-56347-342-5, American Institute of Aeronautics and Astronautics.
- Greg Milner, “Pinpoint: How GPS is Changing Technology, Culture, and Our Minds“
- Neil Ashby & Marc Weiss, NIST Technical Note 1385, “Global Position System Receivers and Relativity”
- Pennsylvania State University, John A. Dutton e-Education Institute, “The GPS Signal”
- Maxim Integrated, Application Note 3447, “Complete Stand-Alone GPS Receiver Solution with MAX2742”
- STMicroelectronics, STA8088CWG Data Sheet
- STMicroelectronics, GNSS, UM2399 User Manual
- EEWorld Online, “Open-source GPS/GNSS-aided inertial navigation software stack handles precise navigation apps”
- EEWorld Online, “Autonomous vehicles: “We don’t need (necessarily) no stinkin’ GPS”
- EEWorldon Online, “Multi-constellation antenna targets automotive apps for location tracking, GPS, GLONASS, and BeiDou bands”