Quartz crystals and oscillators, Part 1: Crystal basics

An oscillator or clock function is key to nearly all electronic circuits, and in most (but not all) cases, the heart of this oscillator circuit is a tiny piece of quartz, called the crystal blank or slab. It’s easy and commonplace to think of the crystal as a simple component, but as with most components, that’s misleading and incorrect; there are many aspects to the material itself, and how itis used, regardless of the application and electronics. This FAQ will look at the quartz-crystal blank itself, and some of the subtleties and variabilities the crystal can undergo.

There are alternatives to the quartz-based crystal, such as are MEMS-based resonators which are gaining increasing market share, and very simple LC-resonant “tank” circuits for low-end applications and with low-modest performance objectives.

Q: For how long have quartz crystals been used in circuits as frequency-setting elements?

A: Since the early part of the 20^th century. Although the piezoelectric effect which they exploit (discussed below) was well-known well before that, there was no place for these quartz elements, as radio and electronics did not exist.

Q: Where does the quartz come from?

A: For many decades, mined natural quartz was the sole option, much of it from Brazil. The quartz was cut along specific crystalline axes and then polished. However, since the 1970s, synthetic quartz crystals have been grown much like silicon ingots (and using many of the same techniques and processes). This results in closer-to-perfect crystalline structures, which yield greatly improved, more consistent performance.

Q: How important are these crystals for determining frequency?

A: Very, very important. They are used extensively for generating system clocks, as well as establishing a single master frequency in a transmitter and receiver, with all needed carrier channels then derived via a synthesizer. Before the availability of such tuning, a radio could be tuned one of two ways: either by manual LC tuning using a knob and dial or by a using a crystal to establish each channel frequency. The former was low cost but inexact; the latter was exact but needed many crystals. In World War II, having the right crystals was so important that the Army Corp of Engineers has a special team of skilled crystal “grinders” whose sole job was to cut, grind, and tune crystals for the military radio channels, and change them as needed.

The development of frequency synthesizers changed the need for and use of crystals. For example, in the 1970s, Citizen’s Band radio was very popular with 23 full-duplex channels assigned in the 27-MHz band. Some “full-band” radios carried 23 transmit- and 23 receive-channel crystals (a total of 46) to access any and all assigned channels; other radios had slots for just two to six crystal pairs, and users would have to physically remove and replace the crystals if they wanted to go to other channels. In contrast, with a synthesized radio, only one master crystal is needed.

Q: What’s the basic principle of the oscillator based on a quartz crystal?

A: It is yet another manifestation of the piezoelectric effect, which characterizes a duality: when a crystal (not necessarily quartz) is subject to an electric field (a voltage), its dimension change in reversible action; when a crystal is stressed, it produces a small voltage. This principle is used in piezoelectric actuators, small audio speakers, pressure sensors, and numerous other applications.

Q: How does a quartz blank become an oscillator?

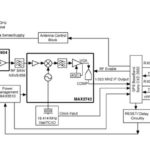
A: The quartz blank is used in an oscillator circuit as the resonating element. When subject to a voltage potential, it will begin to vibrate and oscillate at its “fundamental frequency.” It’s a mutual relationship: the electrical circuit supports the mechanical resonance and vice versa. The crystal is used in the feedback loop of the oscillator to constrain the oscillator’s frequency, Figure 1.

crystals — Fig 1: The many steps from raw quartz-crystal blank to packaged final unit require precision and perfection. (Image source: Slideshare.net)

Q: What types of circuits are used for the oscillator?

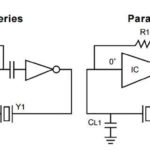
A: There are many topologies in use, among the better known are the Hartley, Pierce, and Colpitts oscillators. Each arrangement has tradeoffs in terms of complexity, cost, stability, and compatibility with the electrical characteristics of the quartz blank. Understanding these characteristics is critical to a high-performance oscillator circuit, including whether the crystal is used in a series- or parallel-resonant mode.

Q: What are the electrical characteristics of the quartz blank?

A: The crystal material and blank have been intensively studied electrically, mechanically, and thermally for decades, as their performance is so critical in many systems. The mechanical model, Figure 2, and electrical model, Figure 3, are closely aligned. The electrical model will have increasing detail as electrical parasitics, and subtle mechanical attributes are added, and as frequency increases and the blank gets smaller.

Fig 2: The simplified mechanical model of the quartz slab is the basis for the electrical equivalent model; this model gets increasingly complicated as more fidelity is desired. (Image source: Maxim Integrated)

Fig 3: The electrical model is an analog of the mechanical model, and is essential to developing a suitable, high-performance oscillator circuit. (Image source: Maxim Integrated)

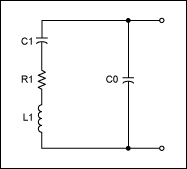
Q: What is the operating frequency range of a crystal-based oscillator?

A: Depending on the quartz blank’s dimensions and associated oscillator, it can range from about 50 kHz and several tens of MHz. Above that, the quartz blank becomes so thin (to achieve a higher natural mechanical resonance) that it is brittle and breaks during normal use.

Q: So how do you generate frequencies below or above that range?

A: You can use a divider or phase-locked loop (PLL) to down convert; for conversion, you can also use a PLL. Before the availability of PLLs and synthesizers, there was another solution: crystals and their oscillators were designed to operate with many harmonic overtones, and then filtering was used to select the 3^rd or 5^th harmonic instead of the fundamental resonance. This provides a solution but requires careful selection of the crystal blank type and characteristics, as well as the oscillator circuit.

Q: Are there standard crystal frequencies?

A: Yes, absolutely. While crystal blanks can be made for almost any frequency within a wide range, there are standard ones available for frequencies such as 100 kHz, 1 MHz, 10 MHz, 3.579545 MHz (often called “3.58 MHz”, needed for now-obsolete analog color TV) and other high-volume, mass-market applications. Personal digital watches and clocks usually use crystal at 32,768 Hz since that frequency can easily be divided down via a flip-flop chain to one pulse/sec (32768 = 2¹⁵).

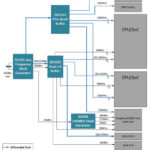
Q: How is the crystal blank physically connected to the circuit?

A: Flat electrodes are packed on the opposing blank faces. These can be thin metal pieces, or they can be electroplated contact surfaces. The assembly is then placed in an enclosure (often metal) to physically protect it and reduce the effect of electrical interference, Figure 4.

Fig 4: Depending on size and application, finished banks are offered in a wide range of packages; most of them are hermetic to protect the blank and assist in achieving consistent performance. (Image source: AOR, LTD)

Q: How large is the quartz blank?

A: It’s a function of the frequency, but a typical medium-frequency crystal blank is anywhere from a few mm square to about 10 mm × 5 mm × 1 mm; some crystals are only a mm or two on each side.

Q: How is the bank adjusted to the desired resonant frequency?

A: By precision grinding and polishing, just as a glass lens would be. For many years this was done by hand by skilled craftspeople; now it is automated, of course, with the preparation and measurement done simultaneously.

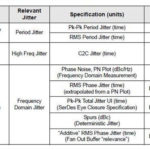
Q: What are the primary performance parameters for a crystal?

A: There are many, of course: initial frequency of resonance, accuracy of that frequency, start-up time, phase noise (jitter), short-term stability (drift), and long-term stability (drift) are among the key ones. Many specifications are presented in parts per million (ppm) or percentage: 0.0001% equals 1 ppm.

Q: What are the drift/stability concerns?

A: Like all mechanical components, quartz blanks change slightly but meaningfully with temperature. Therefore, a shift in ambient or operating temperature of even a few degrees will change their natural resonance and thus their key attributes. Further, as the crystal “ages” in use due to the repeated mechanical stress, the quartz’s attributes change and so does the resonant frequency (it’s analogous to repeated flexing of a metal or peening a metal surface).

Part 2 of this FAQ will discuss the performance of crystal-based oscillators and what can be done to get higher performance, as well as maintain initial accuracy over time and temperature. These factors are critical to the performance of the circuit and application.

There are countless technical papers, treatises, application notes, vendor tutorials, and other support material available thus very important topic. Some are highly readable and applicable, while others take a dive deep into basic physics (this does not mean there are of little use; they are very useful). Among the many are these: