In Part 1, we looked at some facets of noise: sources, external versus internal (intrinsic) noise, and equations. Part 2 goes further into noise specifics.

Q: What are some of the types of noise?

A: It’s a long list. The same noise may have different names depending on the perspective of the person describing it, as well as the application. Among the many entries are:

• Thermal noise, also called Johnson–Nyquist or just Nyquist noise, is an unavoidable noise created by the random thermal motion of charge carriers (usually electrons) within conductors;
• Shot noise is due to the random statistical fluctuations of the electric current when the charge carriers cross a gap. If electrons flow across a barrier, then they have discrete arrival times, and this constitutes at type of noise;
• Flicker noise, also known as 1/f noise, is a signal or process with a spectrum that falls off steadily into the higher frequencies and is caused by a variety of mechanisms;
• Burst noise consists of sudden “step-like” transitions between two or more discrete voltage or current levels, and can reach several hundred microvolts, occurring at random. Each such shift in offset voltage or current lasts from a brief period of several milliseconds to a much-longer period of seconds. It is easily heard in audio circuits where it also known a popcorn noise, for obvious reasons;
• Impulse (or spike) noise is usually caused by nearby electrical circuits and systems, such as when motors or other large loads start/stop, or when brushed motors generate sparks during normal operation; lightning is also a source.
• Switching noise is caused by on/off action of components such as MOSFETs in switching DC/DC regulator;
• Clock noise is due to the fast rise/fall times of a system’s clock generator;
• Static is general atmospheric noise from multiple sources which adds to the desired signal.

Again, these are just a few of the many types and sources of noise.

Q: Do only active devices generate internal noise?

A: Absolutely not. All components – active and passive – are noise sources to some extent, depending on their temperature, construction, and application. Even the basic, simple resistor is a noise source (proportional to the resistance value) so lower-value resistors are used in designs where noise is a limiting factor in performance. In fact, resistors are offered with special materials and fabrication which minimizes the internal noise sources (except for thermal noise, which is unavoidable) .

Active devices do contribute multiple types of noise, and this noise is quantified by parameters such as noise figure and noise temperature, see References 1 and 2.

Q: What are some further mathematical insights into noise, in addition to its rms or peak value?

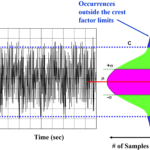
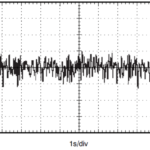
A: The most common type of noise is commonly known as “white noise” which has a flat power spectral density across the spectrum; thermal noise is a good example. The amplitude of the noise signal has a Gaussian probability density function, or very nearly so, Figure 1. When modeling a channel with thermal noise, it is often called an additive white Gaussian noise (AWGN) channel, Figure 2.

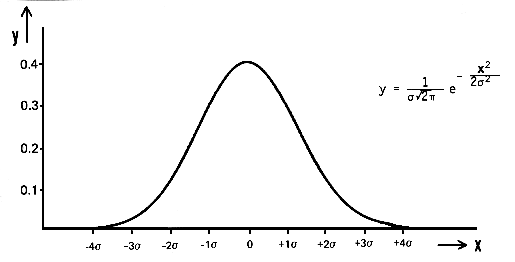
White noise is the most commonly used noise in design analysis for two reason: many real-world physical processes and channels do, in fact, have white noise; also, it is the easiest type of noise to mathematically analyze and model even if it is a simplification and approximation.

Q: Is there another noise “colors” besides white noise?

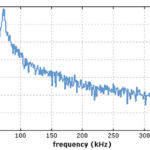
A: Another common noise is called “pink noise,” which has equal energy per octave, and so has more low-frequency components than white noise, Figure 3 (again, white noise has equal energy per frequency interval). Its power spectral density (energy or power per frequency interval) is inversely proportional to the frequency of the signal.

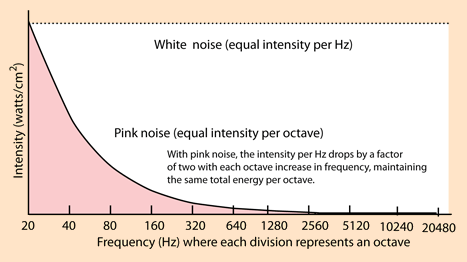
For pink noise, each octave (halving/doubling in frequency) carries an equal amount of noise energy. Pink noise is often seen in the statistical variations of physical and biological systems, and is common in audio systems and channels as it matches the reality of how sounds are perceived (in octave ranges, rather than equal energy per frequency interval).

Q: Does all noise types have a zero mean? 

A: While most types of noise do have zero mean (that’s why their rms value is used, not their average), there are other noise distributions. For example, a unique type of noise called Rician noise (named after Stephen Rice, who analyzed it in 1944) has a complex amplitude distribution characteristic that is not zero mean; despite is unusual nature, it does have real-world aspects, as it is the type of noise seen in MRI data, Reference 5.

Q: Is the “rms average” or peak value of noise constant in an application?

A: Sometimes yes, but more often it is no. For some types of noise, such as thermal noise, it generally is, as the noise is largely a function of temperature. But for many types, it varies with time of day and other external factors. For example, as more motors and appliances are turned on during the day, the impulse noise they create increases; similarly, when circuit subfunctions go from power-saving quiescent state to their active state, the noise they may generate increases. Also, atmospheric noise varies with Sun’s position and day/night changes.

Q: Are all noises fully characterized solely by first-order probabilistic moments (parameters) such as peak or rms value?

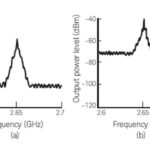
A: Most are, but there are some noise types which need further definition and thus additional moments. For example, there is cyclostationary noise where the first-order moment of rms or peak is not constant but is actually periodic in a predictable cycle, Reference 6. Such noise occurs, for example, when a radar antenna rotates: when it points towards one area, the noise may consistently be less, while in another direction is consistently worse (likely due to the nature of the regions to which it is pointing). Another example is an antenna pointing at the sky, as it will have noise which is periodic with the Earth’s rotation and the location of the Sun. This cyclostationary noise can be properly characterized by using not only the rms and peak values (first moment), but also their periodicity (second moment).

Q: How do you minimize/eliminate noise?

A: Just a noise is a huge topic, dealing with it is also a huge topic and best discussed for another time. Noise reduction depends on the noise source, type, “recipient,” circuit design, system design, and many other factors.

This FAQ has looked briefly at the broad, multifaceted, and very critical topic of noise: its sources, types, descriptions, designations, and analytics. It is a topic for which there are innumerable credible references of all types and intensities ranging from basic qualitative to highly sophisticated and analytical.

No basic or single article can capture all its aspects. Fortunately, there is a substantial amount of useful information examining how to identify the noise sources and their paths, how to deal with them, measuring noise parameters, minimizing noise at its source, reducing its effects at the recipient, and even accommodating it via the use of signal encoding, modulation, and error detection/correction techniques.

References

1. EE World, “RF/microwave noise, Part 1: Noise figure basics”
2. EE World, “RF/Microwave noise, Part 2: Noise temperature and applications”
3. Tektronix, “How can I measure and calculate nV/Root Hz (nanovolt per root Hertz) on a spectrum analyzer?“
4. Texas Instruments, AN-104, “Noise Specs Confusing?”
5. National Institutes of Health, “The Rician Distribution of Noisy MRI Data”
6. Cadence Design Systems, “Cyclostationary Noise in RF Circuits”
7. Simon Fraser University (Canada), “Gaussian Noise or Gaussian Probability Distribution”